Cách Đọc Bảng Công Thức Lượng Giác Cực Dễ Nhớ

Bắt đầu cấp 3 là giai đoạn học sinh lần đầu tiên được tiếp cận với góc lượng giác. Và đây cũng là viên gạch đặt nền móng đầu tiên cho các kiến thức mà học sinh tiếp thu sau này. Do đó, việc nắm vững các công thức lượng giác rất quan trọng trong quá trình học tập. Biết được sự lo lắng đó thì bài viết dưới đây sẽ tổng hợp các công thức thông dụng cần nhớ. Cũng như chỉ cách làm thế nào để học các công thức một cách nhanh nhất cho bạn.

Mục Lục Bài Viết

Khái niệm về lượng giác

Trước khi tìm hiểu về các công thức lượng giác thông dụng thì chúng ta sẽ tìm hiểu khái niệm về lượng giác. Theo cách hiểu đơn giản nhất thì lượng giác là một nhánh toán học. Chúng được ra đời nhằm mục đích tìm hiểu về mối liên hệ giữa hình tam giác và góc độ của nó. Bên cạnh đó, chính lượng giác sẽ giúp chỉ ra hàm số lượng giác. Các hàm số lượng giác thì diễn tả rõ hơn các mối liên kết và có thể áp dụng được trong các hiện tượng có chu kỳ.

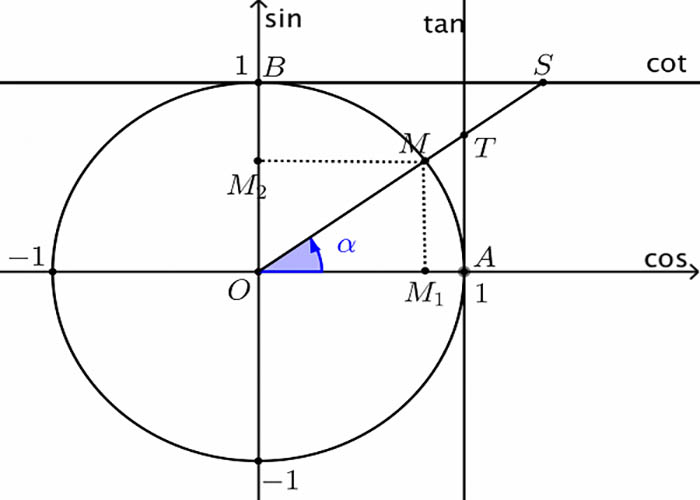
Các công thức lượng giác thông dụng đáng nhớ nhất

Có rất nhiều công thức từ cơ bản đến nâng cao từ sơ cấp đến cao cấp khi nói về lượng giác. Tuy nhiên, dưới đây là một vài công thức cơ bản thông dụng đáng nhớ nhất:

Công thức lượng giác cơ bản

$1.\ \tan x=\frac{\sin x}{\cos x}$

$2.\ \cot x=\frac{\cos x}{\sin x}$

$3.\ \sin^2x+\cos^2x=1$

$4.\ \tan x.\cot x=1\left(x\ne k\frac{\pi}{2},\ k\ ∈\ Z\right)$

$5.\ 1+\tan^2x=\frac{1}{\cos^2x}\ \left(x\ne\frac{\pi}{2}+k\pi,\ k\ ∈\ Z\right)$

$6.\ 1+\cot^2x=\frac{1}{\sin^2x}\ \left(x\ne k\pi,\ k\ ∈\ Z\right)$

1. sin (a ± b) = sin a.cos b ± cos a.sin b

2. cos (a + b) = cos a.cos b – sin a.sin b

3. cos (a – b) = cos a.cos b + sin a.sin b

$4.\ \tan\left(a+b\right)=\frac{\tan a+\tan b}{1-\tan.\tan b}$

$5.\ \tan\left(a-b\right)=\frac{\tan a-\tan b}{1+\tan a.\tan b}$

Mẹo nhớ công thức cộng: Sin thì sin cos cos sin, cos thì cos cos sin sin dấu trừ. Tan thì tan nọ tan kia chia cho mẫu số 1 trừ tan tan.

Công thức các cung liên kết trên đường tròn lượng giác

Mẹo nhớ: cos đối, sin bù, phụ chéo, tan hơn kém π

Hai góc đối nhau:

cos (-x) = cos x
sin (-x) = -sin x
tan (-x) = -tan x
cot (-x) = -cot x

Hai góc bù nhau:

sin (π – x) = sin x
cos (π – x) = -cos x
tan (π – x) = -tan x
cot (π – x) = -cot x

Hai góc phụ nhau:

sin (π/2 – x) = cos x
cos (π/2 – x) = sin x
tan (π/2 – x) = cot x
cot (π/2 – x) = tan x

Hai góc hơn kém π:

sin (π + x) = -sin x
cos (π + x) = -cos x
tan (π + x) = tan x
cot (π + x) = cot x

Hai góc hơn kém π/2:

sin (π/2 + x) = cos x
cos (π/2 + x) = -sin x
tan (π/2 + x) = -cot x
cot (π/2 + x) = -tan x

Công thức nhân

Công thức nhân đôi:

sin2a = 2sina.cosa
cos2a = cos²a – sin²a = 2cos²a – 1 = 1 – 2sin²a
$\tan2a=\frac{2\tan a}{1-\tan^2a}$
$\cot2a=\frac{\cot^2a\ -1}{2\cot a}$

Công thức nhân ba:

sin3a = 3sina – 4sin³a
cos3a = 4cos³a – 3cosa
$\tan3a=\frac{3\tan a-\tan^3a}{1-3\tan^2a}$
$\cot3a=\frac{\cot^3a-3\cot a}{3\cot^2a-1}$

Công thức nhân bốn:

sin4a = 4.sina.cos³a – 4.cosa.sin³a
cos4a = 8.cos⁴a – 8.cos²a + 1
hoặc cos4a = 8.sin⁴a – 8.sin²a + 1

Công thức hạ bậc

Thực ra những công thức này đều được biến đổi ra từ công thức lượng giác cơ bản, ví dụ như: sin²a=1 – cos²a = 1 – (cos2a + 1)/2 = (1 – cos2a)/2.

$1.\ \sin^2a\ =\ \frac{1-\cos2a}{2}$

$2.\ \cos^2a=\frac{1+\cos2a}{2}$

$3.\ \sin^3a=\frac{3\sin a-\sin3a}{4}$

$4.\ \cos^3a=\frac{3\cos a+\cos3a}{4}$

Công thức biến tổng thành tích

Mẹo nhớ: cos cộng cos bằng 2 cos cos, cos trừ cos bằng trừ 2 sin sin; sin cộng sin bằng 2 sin cos, sin trừ sin bằng 2 cos sin.

$1.\ \cos a+\cos b=2\cos\frac{a+b}{2}.\cos\frac{a-b}{2}$

$2.\ \cos a-\cos b=-2\sin\frac{a+b}{2}.\sin\frac{a-b}{2}$

$3.\ \sin\ a+\sin b=2\sin\frac{a+b}{2}.\cos\frac{a-b}{2}$

$4.\ \sin\ a-\sin b=2\cos\frac{a+b}{2}.\sin\frac{a-b}{2}$

$5.\ \tan a+\tan b=\frac{\sin\left(a+b\right)}{\cos a.\cos b}$

$6.\ \tan a-\tan b=\frac{\sin\left(a-b\right)}{\cos a.\cos b}$

$7.\ \sin a+\cos a=\sqrt{2}\sin\left(a+\frac{\pi}{4}\right)=\sqrt{2}\cos\left(a-\frac{\pi}{4}\right)$

$8.\ \sin a-\cos a=\sqrt{2}\sin\left(x-\frac{\pi}{4}\right)=-\sqrt{2}\cos\left(x+\frac{\pi}{4}\right)$

$9.\ \tan a+\cot a=\frac{2}{\sin2a}$

$10.\ \cot a-\tan a=2\cot2a$

$11.\ \sin^4a+\cos^4a=1-\frac{1}{2}\sin^22a=\frac{1}{4}\cos4a+\frac{3}{4}$

$12.\ \sin^6a+\cos^6a=1-\frac{3}{4}\sin^22a=\frac{3}{8}\cos4a+\frac{5}{8}$

Công thức biến đổi tích thành tổng

$1.\ \cos a.\cos b=\frac{1}{2}\left[\cos\left(a+b\right)+\cos\left(a-b\right)\right]$ $2.\ \sin a.\sin b=-\frac{1}{2}\left[\cos\left(a+b\right)-\cos\left(a-b\right)\right]$

$3.\ \sin a.\cos b=-\frac{1}{2}\left[\sin\left(a+b\right)+\sin\left(a-b\right)\right]$

Nghiệm phương trình lượng giác

Phương trình lượng giác cơ bản:

$1.\;\sin a=\sin b\;\Leftrightarrow\left[\begin{array}{c}a=b+k2\mathrm\pi\\a=\mathrm\pi-\mathrm b+\mathrm k2\mathrm\pi\end{array}(k\in Z)\right]$

$2.\;\cos a=\cos b\;\Leftrightarrow\;\left[\begin{array}{c}a=b+k2\mathrm\pi\\a=-b+k2\mathrm\pi\end{array}(k\in Z)\right]$

3. tan a = tan b ⇔ a = b + kπ; (k ∈ Z)

4. cot a = cot b ⇔ a = b + kπ; (k ∈ Z)

Phương trình lượng giác trong trường hợp đặc biệt:

sin a = 0 ⇔ a = kπ; (k ∈ Z)
sin a = 1 ⇔ a = π/2 + k2π; (k ∈ Z)
sin a = -1 ⇔ a = -π/2 + k2π; (k ∈ Z)
cos a = 0 ⇔ a = π/2 + kπ; (k ∈ Z)
cos a = 1 ⇔ a = k2π; (k ∈ Z)
cos a = -1 ⇔ a = π + k2π; (k ∈ Z)

9. Dấu của các giá trị lượng giác

Góc phần tư số	I	II	III	IV
Giá trị lượng giác	I	II	III	IV
sin x	+	+	–	–
cos x	+	–	–	+
tan x	+	–	+	–
cot x	+	–	+	–

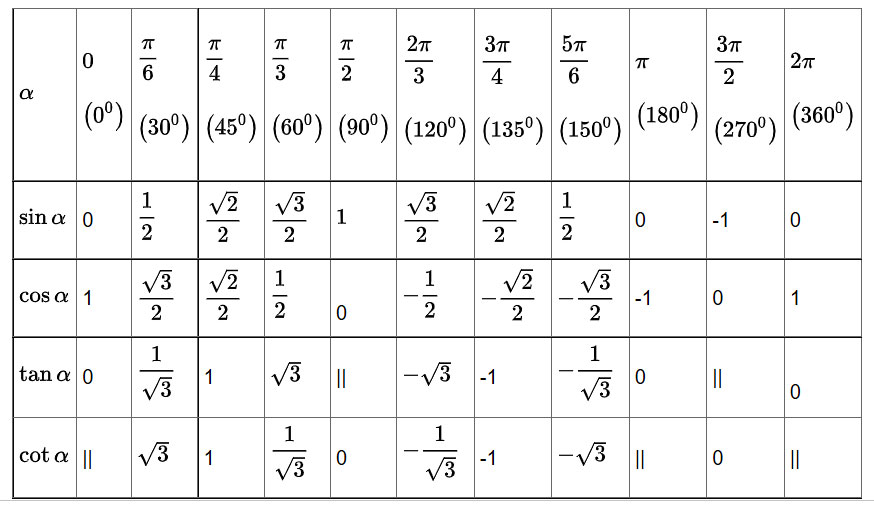
Bảng giá trị lượng giác một số góc đặc biệt

Tỉ số lượng giác của 2 góc phụ nhau. ( α + β = 90°)

sin α = cos β cos α = sin β

tan α = cot β cot α = tan β

Bảng tỉ số của các góc đặc biệt

Công thức lượng giác bổ sung

Biểu diễn công thức theo $t=\frac{\tan a}{2}$

$1.\ \sin a=\frac{2t}{1+t^2}\ \ \ \ \ \ \ \ \ \ \ \ 2.\ \cos a=\frac{1-t^2}{1+t^2}$

$3.\ \tan\ a=\frac{2t}{1-t^2}\ \ \ \ \ \ \ \ \ \ 4.\ \cot a=\frac{1-t^2}{2t}$

Làm thế nào để tiếp thu được công thức lượng giác một cách nhanh chóng nhất?

Có quá nhiều công thức cần phải nhớ và rất dễ lẫn lộn chúng. Vậy phải làm sao mới có thể tiếp thu được các công thức này một cách dễ dàng đây. Bạn có thể tham khảo một vài cách học lượng giác sau nhé:

Thường xuyên làm bài tập và vẽ thật nhiều

Việc này sẽ giúp bạn hiểu rõ bản chất của công thức lượng giác hơn. Từ đó công thức sẽ tự động được lưu vào tâm trí bạn. Và bạn cũng có thể dễ dạng biết cách áp dụng chúng cho những bài tập tiếp theo.

Học các công thức thông qua các bài thơ

Hiện nay, để hỗ trợ cho việc học thì các thầy cô cũng như những học sinh đi trước đã sáng tác rất nhiều bài thơ. Việc này sẽ giúp việc học công thức của bạn không trở nên quá nhàm chán.

Một số bài thơ

“ Sin thì Sin Cos Cos Sin

Cos thì Cos Cos Sin Sin dấu trừ

Tan thì Tan cộng chia 1 trừ Tan nhân”

“ Nhân 3 một góc bất kỳ

Sin thì 3 4, Cos thì 4 3.

Dấu trừ đặt giữa hai ta

Lập phương đổi chỗ thế là ra ngay”

Ứng dụng của công thức lượng giác trong đời sống hiện nay

Việc học các công thức ở trường chủ yếu để tăng khả năng tư duy logic cho học sinh. Tuy nhiên, nếu bạn là người học chuyên sâu thì bạn sẽ nhận ra các công thức này còn có thể nâng cao hơn. Đồng thời chúngđược vận dụng vào thực tế nhiều hơn. Dưới đây là một vài ứng dụng của công thức lượng giác trong đời sống:

Thiết kế các công trình hạ tầng ( chủ yếu là thiết kế cầu)

Có thể bạn không biết, các thiết kế của cây cầu được áp dụng rất nhiều kiến thức về khối lượng, trọng lực,…ở các góc độ khác nhau. Và khi hoàn thành bạn sẽ nhận ra chúng có nhiều hình tam giác và lượng giác. Việc thiết kế này nhằm tăng sự kết hợp giữa độ dài và độ vững chắc của cầu.

Thiết kế ra định vị vị trí GPS

Một điều thú vị nữa có lẽ bây giờ bạn mới biết đó là việc sáng chế ra định vị GPS là dựa vào kiến thức lượng giác. Việc sử dụng này có thể cho chúng ta biết chính xác vị trí của mình cũng như nơi mình cần đến. Kết hợp với các dữ liệu từ vệ tinh và hình học trái đất. Thì lượng giác sẽ xác định được kinh độ và vĩ độ của bạn.

Một bản nhạc

Bạn không nhìn lầm đâu, thực tế là quá trình tạo ra một bài hát cũng là một trong những kiến thức về lượng giác đấy. Cụ thể hơn bạn có thể nhìn thấy chính là hình của sóng nhạc. Từ việc ghi âm kỹ thuật số cho đến việc nén thành dạng MP3. Thì đều đòi hỏi kiến thức nhất định và chuyên sâu về lượng giác.

Máy trắc địa

Đối với những người làm trong lĩnh vực xây dựng có lẽ đã quá quen với chiếc máy này. Chúng được áp dụng kiến thức về lượng giác để đo đạc và mô phỏng 3D công trình xây dựng. Quá trình cụ thể bao gồm việc xác định các góc cạnh và hướng gió. Cũng như việc tính toán đặt các tấm năng lượng mặt trời nhằm mang đến hiệu suất cao nhất.

Hy vọng với các thông tin về công thức lượng giác có thể giúp ích được cho bạn. Mong rằng bạn sẽ sớm tìm được cách và phương pháp học tốt nhất cho mình.